Memoization (a key concept in dynamic programming) is a fancy word that basically means storing the results of computation and never recomputing. Instead, you simply look up the already computed value. Any pure function can be memoized.
Memoization can have a dramatic affect on the runtime of algorithms which use the results of computation multiple times.
A classic example:
The Fibonacci sequence is a famous and very old sequence of numbers given by:
$$
\begin{align}
F_0 &= 1 \\
F_1 &= 1 \\
F_n &= F_{n-1} + F_{n-2} \\
\end{align}
$$
This sequence has interesting connections to all kinds of mathematics, but that’s another post altogether.
For now, lets implement it in python!
Here is a definition that is quite faithful to its mathematical definition:
def fib(n):
return 1 if n < 2 else fib(n - 1) + fib(n - 2)
Elegant and unquestionably correct.
Lets take it for a test drive.
print [fib(n) for n in xrange(10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
Cool! That seems to be working well.
Wait. How well does this perform?
%timeit fib(35)
1 loop, best of 3: 3.39 s per loop
Holy cow that’s slow!
To understand why, take a look at the call graph of fib(6):
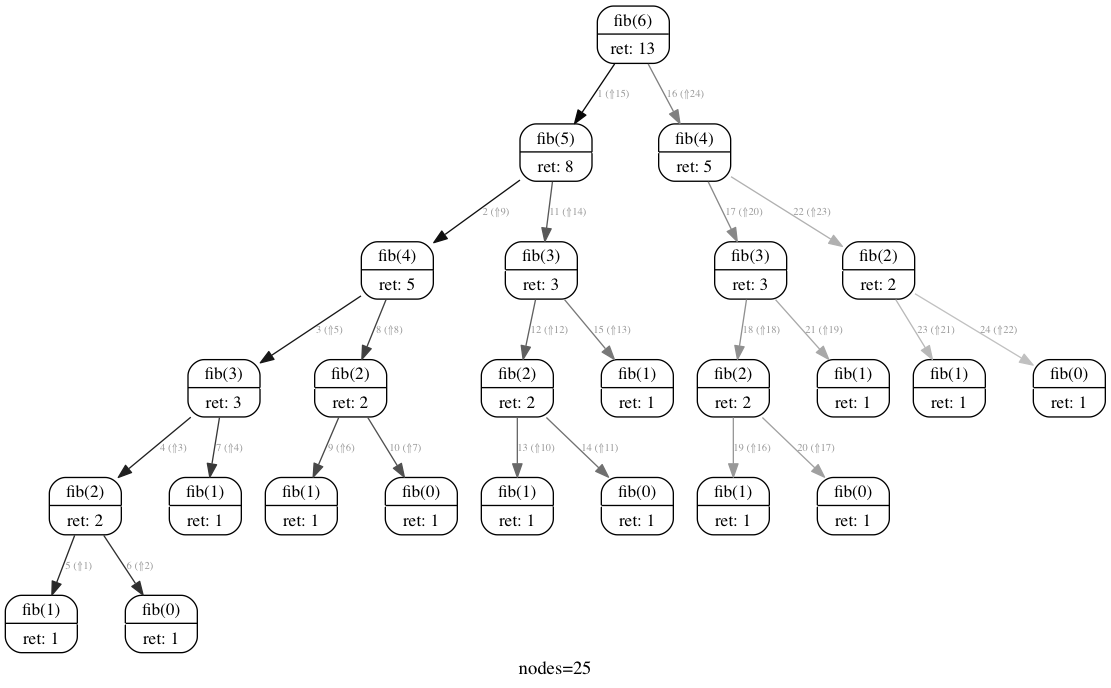
Take a look at all that recomputation! It’s diabolical! All we really need is the far left depth first traversal, but the algorithm has no way of knowing that.
Let’s fix that.
memoized_fib_values = {}
def memoized_fib(n):
if n < 2:
return 1
if memoized_fib_values.get(n):
return memoized_fib_values[n]
memoized_fib_values[n] = memoized_fib(n - 1) + memoized_fib(n - 2)
return memoized_fib_values[n]
print [memoized_fib(n) for n in xrange(10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
Ok, so far so good. How much better is our performance?
%timeit memoized_fib(35)
The slowest run took 122.39 times longer than the fastest. This could mean that an intermediate result is being cached.
1000000 loops, best of 3: 261 ns per loop
Hmmm. That’s an interesting result. The %timeit function noticed that there was a huge difference between the slowest and the fastest run. That’s because %timeit runs the code a bunch of times to give you a more accurate result. In our case, once memoized_fib(35) was computed once, it was never computed again. Further function calls were simply a dictionary lookup.
Let’s roll our own timing function to get a feel for how much we gained.
import time
def simple_timeit(f, *args, **kwargs):
initital_time = time.time()
f(*args, **kwargs)
print '{} took {} miliseconds'.format(f.__name__, (time.time() - initital_time) * 1000)
memoized_fib_values = {}
simple_timeit(fib, 35)
simple_timeit(memoized_fib, 35)
simple_timeit(memoized_fib, 35)
fib took 3429.04305458 miliseconds
memoized_fib took 0.0250339508057 miliseconds
memoized_fib took 0.000953674316406 miliseconds
Awesome!
The memoized version of fib took about five orders of magnitude less time than the original! (We changed the runtime of the algorithm from exponential to linear.)
Also, note that the second call to memoized_fib was an order of magnitude faster than the first call. That’s because it was just a dictionary lookup.
While the performance benefits are impressive, the implementation of the memoized version leaves something to be desired. It relies on a global dictionary to store computation results and it has lost the simple elegance and mathematical purity of the original implementation.
Is it possible to have the best of both worlds?
Yes, yes it is. 🙂
Let’s write a decorator to abstact away all the gory details of memoization.
import functools
def memoize(f):
computed = {}
@functools.wraps(f)
def memoized_f(main_arg, *args, **kwargs):
if computed.get(main_arg):
return computed[main_arg]
computed[main_arg] = f(main_arg, *args, **kwargs)
return computed[main_arg]
return memoized_f
memoize is a higher order function and so we can use it as a decorator.
Note that memoized_f is a closure and it captures the computed variable. This eliminates the need for a global variable to hold the computed values.
Also, note the *args and **kwargs parameters. This allows functions which take more than one parameter and functions that take keyword arguments to be decorated with @memoize. However, it is important to take note that the memoized computation is determined solely by the main_arg parameter. i.e., if you decorate a function with @memoize that takes multiple arguments, you had better always call that function with those parameters if they change the resulting value or else you will get incorrect results.
If you wanted, you could modify memoize to set the keys to computed to be some combination (or a hash) of all the parameters, but I’ll leave that as an exercise for the reader.
For now, lets try out the decorator!
@memoize
def fib(n):
return 1 if n < 2 else fib(n - 1) + fib(n - 2)
simple_timeit(fib, 35)
simple_timeit(fib, 35)
fib took 0.191926956177 miliseconds
fib took 0.000953674316406 miliseconds
Sweet!
Now we have the elegance of the original and the performance of the hand-crafted memoized version. We also have a reusable tool that can apply to any pure function. If you determine that a particular function is causing you a performance hit, consider memoization.
Lets look at one last example.
We can apply the @memoize decorator to any function we want!
Lets consider the math.factorial function:
from math import factorial
memoized_factorial = memoize(factorial)
print "math.factorial(100000) runtimes:"
simple_timeit(factorial, 100000)
simple_timeit(factorial, 100001)
print "\nmemoized(math.factorial(100000)) runtimes:"
simple_timeit(memoized_factorial, 100000)
simple_timeit(memoized_factorial, 100000)
math.factorial(100000) runtimes:
factorial took 2777.85110474 miliseconds
factorial took 2858.99400711 miliseconds
memoized(math.factorial(100000)) runtimes:
factorial took 2846.65703773 miliseconds
factorial took 0.00190734863281 miliseconds
As you can see, the original version always recomputes the value, but our memoized version just tells us the falue if it already knows the answer.
The tradeoff is that you are storing the computation results in a dictionary.
A better implementation would allow you to set an upper limit on the size of the memoization data structure. It turns out that this is part of the standard library (for Python 3, and there is a back-port for Python 2). It’s in the functools module and it’s called lru_cache. You set the size by passing a keyword argument max_size. It also comes with a way to inspect statistics about cache hits and misses.
I just started Python and I’ve got no idea what memoization is and how to use it. Also, may I have a simplified example?
Given that this post explains what memoization is and how to use it, perhaps you can ask a more specific question?